Wie man Graphen als Datenstruktur abbildet

Dieser Artikel behandelt die Darstellung von Graphen als Array und als HashTable.

Ausgangslage

Vermutlich wissen die Leser dieses Beitrags was ein Graph ist. Falls nicht, hilft Wikipedia. In Lehrbüchern werden Graphen in der Regel graphisch dargestellt, d.h. mit Knoten und Kanten und die ganzen fantastischen Algorithmen werden anhand grafischer Beispiele illustriet. Für ungeübte Entwickler, ist dann der Transfer von der grafischen Darstellung zur Implementierung nicht leicht. Hier soll der nachfolgende Beitrag einen Einstieg bieten.

TL;DR

Graphen mit n Knoten lassen sich als n-mal-n Array oder als HashTable als HashTables (Dict in Python) darstellen. Bei ersterem gibt der Eintrag in den Zeilen/Spaltenkombinationen Auskunft darüber, ob eine Kante zwischen Knoten i und j existiert und ggf. auch Auskunft über das Kantengewicht. Bei der HashTable legen wir Einträge lediglich für existierende Kanten an. Knotengewichte können in einem separaten Array dargestellt werden.

Option a) Darstellung von Graphen als Knoten x Knoten Array

Für einen Graph mit n Knoten:

• implementieren wir ein zweidimensionales Array mit n Einträgen in der ersten Dimension
• und n Einträgen in der zweiten Dimension
• Hierbei repräsentiert der i-te Eintrag in der ersten Dimension einen der nKnoten
• und die jeweiligen Einträge in der zweiten Dimension geben an, ob es eine Kante von i zum j-ten Knoten gibt
• Existiert keine Kante, tragen wir None ein
• Existiert eine Kante geben wir das Kantengewicht an (oder True, falls es keine Kantegewichte gibt)

Option b) Darstellung als HashTable

Für einen Graph mit n Knoten:

• implementieren wir eine HashTable (Python: ein Dict) mit einem Key-Eintrag je Knoten, beispielsweise dessen Bezeichnung
• Für jeden Knoten-Key i in dieser HashTable legen wir dann eine HashTable als Value an.
• Hierbei enthält die jeweilige Kanten-HashTable einen Key für die Knoten, zwischen denen es eine Kante mit i gibt
• Der passende Wert ist dann das Kantengewicht

Vorteil dieser Repräsentation ist, dass wir bei Graphen mit vielen Knoten, aber wenig Kanten, nicht unnütze Einträge erzeugen.

Beispiel: Ungerichteter Graph

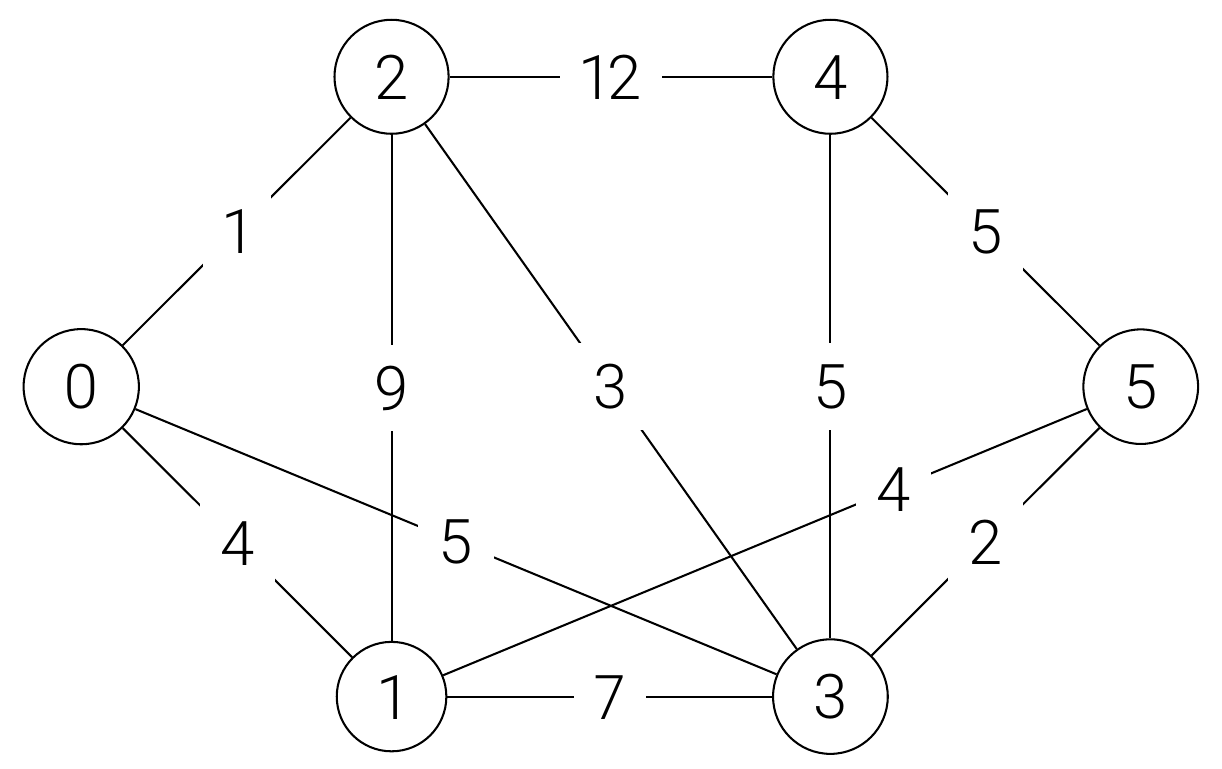
Implementierung als Array

Für jeden der 6 Knoten legen wir ein Array mit je einem potentiellen Eintrag zu den anderen 5 Knoten und zu sich selbst an. Die einzelnen Einträge innerhalb dieser Arrays referenzieren die Knoten. So stellt beispielsweise graph[0][3] die Kante zwischen Knoten 0 und 3 dar. Die Einträge sollen Auskunft über die Existenz einer Kante zwischen dem betrachteten Knoten und den anderen geben. Existiert eine Kante, wird das Kantengewicht eingetragen, existiert keine Kante, schreiben wir None.

graph = [
    [None, 4, 1, 5, None, None], # Kanten von 0 ausgehend
    [4, None, 9, 7, None, 4],    # Kanten von 1 ausgehend
    [1, 9, None, 3, 12, None],   # Kanten von 2 ausgehend
    [5, 7, 3, None, 5, 2],       # Kanten von 3 ausgehend
    [None, None, 12, 5, None, 5], # Kanten von 4 ausgehend
    [None, 4, None, 2, 5, None]     # Kanten von 5 ausgehend
]

Da der Graph ungerichtet ist, haben wir für jede Kante zwischen zwei Knoten einen Eintrag in den beiden betroffenen Arrays (oder auch nicht).

• Der zweite Eintrag in der ersten Liste bildet die Kante zwischen Knoten 0 und 1 mit der Länge 4 ab, d.h. graph[0][1] = 4. Analog dazu finden wir einen Eintrag graph[1][0] = 4.
• Es gibt keine Kante zwischen Knoten 2 und 5 (bzw. 5 und 2), deswegen sind graph[2][5] und graph[5][2] jeweils None.

Implementierung als HashTable

graph = {
    0 : {1 : 4, 2 : 1, 3 : 5}, # Kanten von 0 ausgehend
    1 : {0 : 4, 2 : 9, 3 : 7, 5 : 4}, # Kanten von 1 ausgehend
    2 : {0 : 1, 1 : 9, 3 : 3, 4 : 12}, # Kanten von 2 ausgehend
    3 : {0 : 5, 1 : 7, 2 : 3, 4 : 5, 5 : 2}, # Kanten von 3 ausgehend
    4 : {2 : 12, 3 : 5, 5 : 4}, # Kanten von 4 ausgehend
    5 : {1 : 4, 3 : 2, 4 : 5} # Kanten von 5 ausgehend
}

• Key 0 repräsentiert Knoten 0. In der dahinterliegenden HashTable sind die Kanten zu den Knoten 1 (1 : 4), 2 (2 : 1) und 3 (3 : 5) angegeben.

Beispiel: Gerichteter Graph

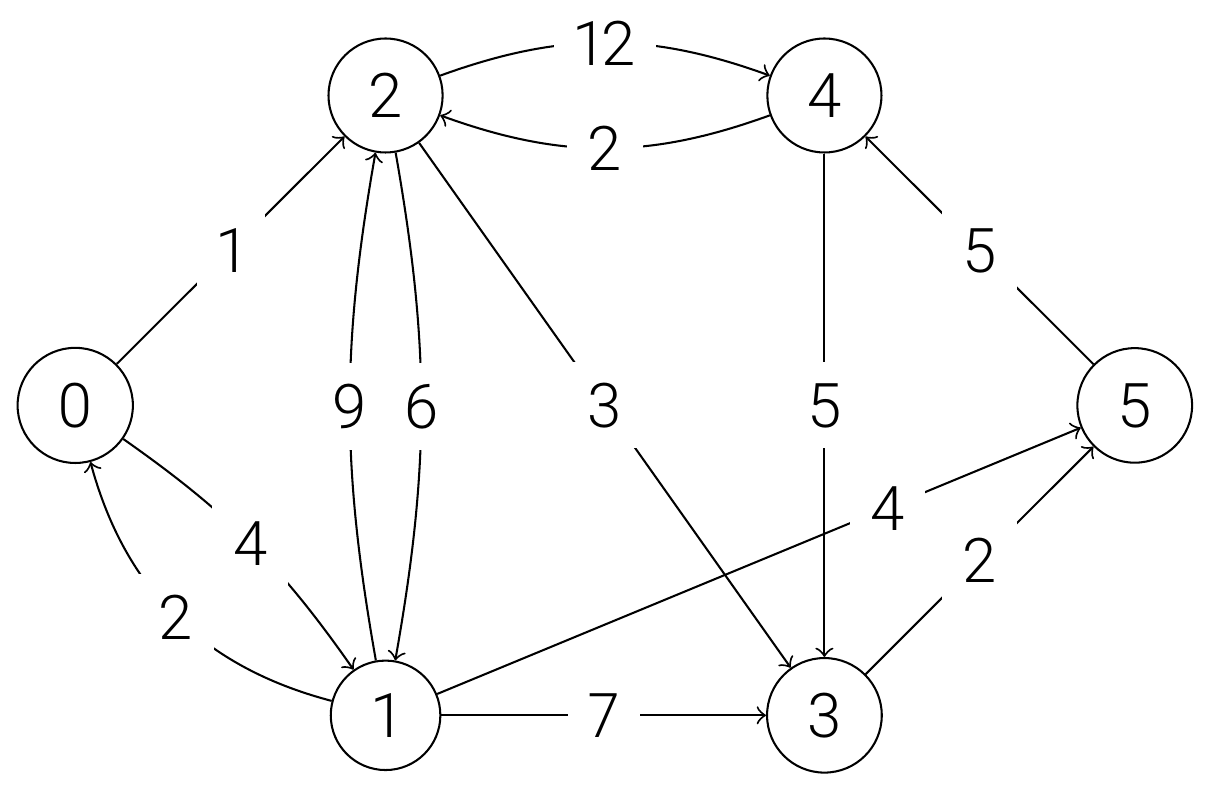
Implementierung als Array

graph = [
    [None, 4, 1, None, None, None], # Kanten von 0 ausgehend
    [2, None, 9, 7, None, 4],       # Kanten von 1 ausgehend
    [None, 6, None, 3, 12, None],   # Kanten von 2 ausgehend
    [None, None, None, None, None, 2], # Kanten von 3 ausgehend
    [None, None, 2, 5, None, None], # Kanten von 4 ausgehend
    [None, None, None, None, 5, None]  # Kanten von 5 ausgehend
]

Der abgebildete Graph ist gerichtet, so dass die Einträge im Array jetzt nur dann numerisch sind, wenn die Richtung der Kante berücksichtigt wird.

• Es gibt eine Kante von 0 zu 1 mit Länge 2, d.h. graph[0][1] = 4. Der Eintrag graph[1][0] unterscheidet sich jetzt jedoch.
• Zwar gibt es eine Kante von 1 zu 3 (graph[1][3] = 7), nicht aber von 3 zu 1 (graph[3][1] = None)

Implementierung als HashTable

graph = {
    0 : {1 : 4, 2 : 1}, # Kanten von 0 ausgehend
    1 : {0 : 2, 2 : 9 3 : 7}, # Kanten von 1 ausgehend
    2 : {1 : 6, 3 : 3, 4 : 12}, # Kanten von 2 ausgehend
    3 : {5 : 2}, # Kanten von 3 ausgehend
    4 : {2 : 2, 3 : 5}, # Kanten von 4 ausgehend
    5 : {4 : 5} # Kanten von 5 ausgehend
}

Im Vergleich zur Darstellung als Array kommen wir mit deutlich weniger Einträgen aus (wenn man None) mit zählt.

Beispiel: Graphen mit nichtnumerischen Knotenbezeichnungen

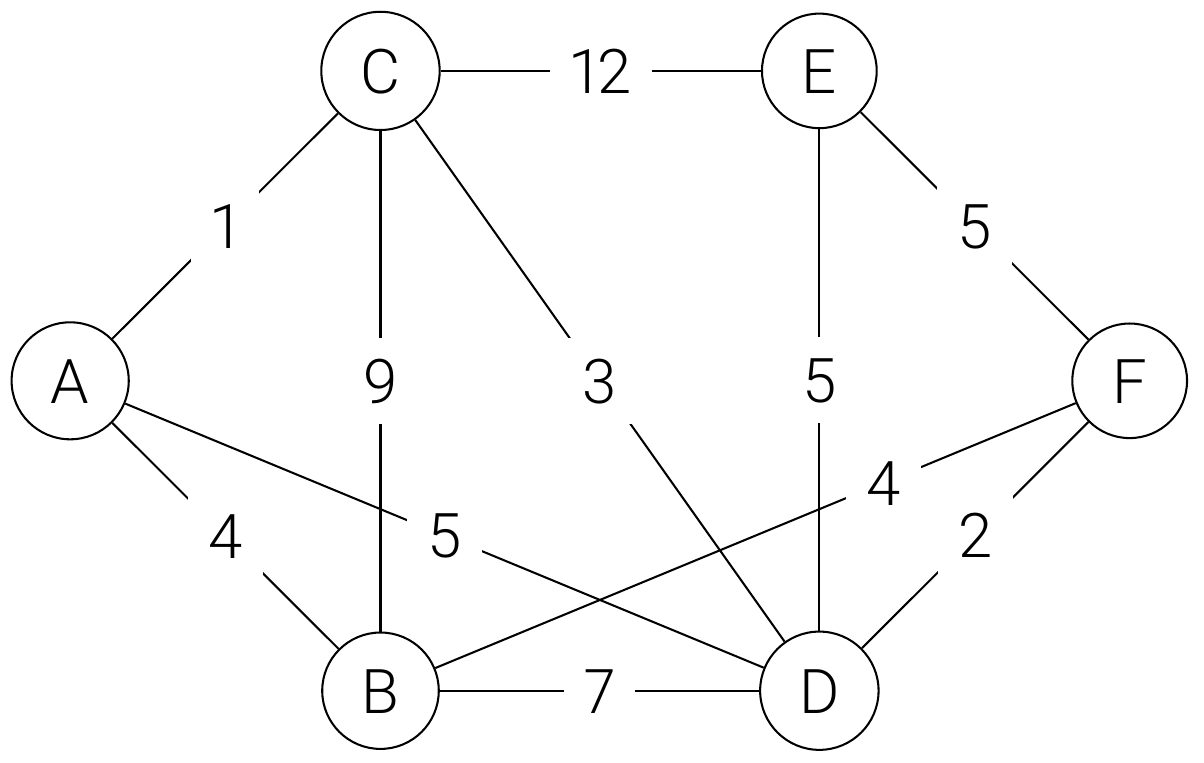
Wenn die Knoten ein nichtnumerische Bezeichnung haben (oder nicht beginnend bei 0 aufsteigend nummeriert sind), helfen wir uns mit einem Dictionary (bzw. einer HashTable), um die Knoten zu identifizieren.

Zunächst legen wir ein Dictionary an, das die Bezeichnung in einen Arrayindex übersetzt:

Implementierung als Array

# Dictionary, A ist Index 0, B ist Index 1 usw.
node_index = {"A" : 0, "B" : 1, "C" : 2, "D" : 3, "E" : 4, "F" : 5 }
graph = [
    [None, 4, 1, 5, None, None], # Kanten von 0 ausgehend
    [4, None, 9, 7, None, 4],    # Kanten von 1 ausgehend
    [1, 9, None, 3, 12, None],   # Kanten von 2 ausgehend
    [5, 7, 3, None, 5, 2],       # Kanten von 3 ausgehend
    [None, None, 12, 5, None, 5], # Kanten von 4 ausgehend
    [None, 4, None, 2, 5, None]     # Kanten von 5 ausgehend
]

Wollen wir dann das Kantengewicht von A zu D abrufen, schreiben wir:

kantengewicht = graph[node_index["A"]][node_index["D"]]

Implementierung als HashTable

graph = {
    "A" : {"B" : 4, "C" : 1, "D" : 5}, # Kanten von 0 ausgehend
    "B" : {"A" : 4, "C" : 9, "D" : 7, "F" : 4}, # Kanten von 1 ausgehend
    "C" : {"A" : 1, "B" : 9, "D" : 3, "E" : 12}, # Kanten von 2 ausgehend
    "D" : {"A" : 5, "B" : 7, "C" : 3, "E" : 5, "F" : 2}, # Kanten von 3 ausgehend
    "E" : {"C" : 12, "D" : 5, "F" : 4}, # Kanten von 4 ausgehend
    "F" : {"B" : 4, "D" : 2, "E" : 5} # Kanten von 5 ausgehend
}

Nichtnumerische Bezeichnungen können als String direkt implementiert werden.

kantengewicht = graph["A"]["B"]

Ergänzung: Graph als Klasse

Es lohnt sich, die Rohstruktur in einer Klasse zu implementieren. Hierbei kann es den Anwendern anschließend egal sein, ob der Graph als Array oder als HashTable implementiert wurde. Die entsprechenden Funktionen erlauben einen abstrakten Zugriff auf die relevanten Funktionen (Kanten hinzufügen, löschen, auslesen).

Graphenklasse auf Arraybasis

class Graph:
    
    def __init__(self, node_labels : list, directed=False):
        """ 
        Implementiert den generischen Array-Fall mit beliebigen Knotenbezeichnern.
        [node_labels] : Liste mit Knotenbezeichnungen.
        Funktion initialisiert leeren Graphen.
        """
        self.nr_nodes = len(node_labels)
        self.__directed = directed
        self.__label_map = {}
        for i, label in enumerate(node_labels):
            # Knoten i entspricht i-tem Label
            self.__label_map[label] = i
        # Initialisiert den leeren Graph
        self.__g = [[None]*self.nr_nodes for _ in range(self.nr_nodes)]

    def edge_exists(self,i,j):
        """ Gibt True zurück, wenn die Kante i,j existiert, ansonsten False """
        index_i = self.__label_map[i]
        index_j = self.__label_map[j]
        return self.__g[index_i][index_j] is not None

    def add_edge(self, i, j, weight):
        """ Fügt Kante (i,j) mit Gewicht 'weight' dem Graph hinzu """
        index_i = self.__label_map[i]
        index_j = self.__label_map[j]
        self.__g[index_i][index_j] = weight
        if self.__directed == False:
            # Ungerichteter Graph
            # Kante in beide Richtungen passierbar
            self.__g[index_j][index_i] = weight

    def remove_edge(self,i,j):
        """ Entfernt Kante (i,j) aus dem Graph """
        self.__g[self.__label_map[i]][self.__label_map[j]] = None
        if self.__directed == False:
            self.__g[self.__label_map[i]][self.__label_map[j]] = None

    def get_weight(self,i,j):
        """ Gibt das Kantengewicht zwischen (i,j) zurück """
        return self.__g[self.__label_map[i]][self.__label_map[j]]

Graphenklasse auf HashTable-Basis

class Graph:
    
    def __init__(self, node_labels : list, directed=False):
        """ 
            Initialisiert leeren HashTable Graph auf Basis der Knotenbezeichnungen.
        """
        self.nr_nodes = len(node_labels)
        self.node_labels = node_labels
        self.__directed = directed

        # Initialisiert den leeren Graph
        self.__g = {}
        for n in node_labels:
            self.__g[n] = {}

    def edge_exists(self,i,j):
        """ Gibt True zurück, wenn die Kante i,j existiert, ansonsten False """
        if i not in self.__g:
            # Knoten existiert nicht
            return False
        # Kante existiert / nicht
        return j in self.__g[i]

    def add_edge(self, i, j, weight):
        """ Fügt Kante (i,j) mit Gewicht 'weight' dem Graph hinzu """
        self.__g[i][j] = weight
        if self.__directed == False:
            # Ungerichteter Graph
            # Kante in beide Richtungen passierbar
            self.__g[j][i] = weight

    def remove_edge(self,i,j):
        """ Entfernt Kante (i,j) aus dem Graph """
        del self.__g[i][j]
        if self.__directed == False:
            del self.__[j][i]

    def get_weight(self,i,j):
        """ Gibt das Kantengewicht zwischen (i,j) zurück """
        return self.__g[i][j]

Beide Varianten funktionieren wie folgt:

• Möglichkeit den Graph kantenlos zu initialisieren
• Angabe, ob der Graph gerichtet ist oder nicht. Ist er ungerichtet, fügen wir später Kanten automatisch zwischen zwei Knoten ein
• Information, ob eine Kante existiert (edge_exists)
• Möglichkeit zum Hinzufügen und Entfernen von Kanten
• Abruf der Kantengewichte

Wenn wir diese Implementierung verwenden wollen, um den oben abgebildeten ungerichteten Graphen mit numerischer Knotenbezeichnung zu implementieren, gehen wir wie folgt vor:

knoten = [0,1,2,3,4,5]
kantengewichte = [
    [None, 4, 1, 5, None, None], # Kanten von 0 ausgehend
    [4, None, 9, 7, None, 4],    # Kanten von 1 ausgehend
    [1, 9, None, 3, 12, None],   # Kanten von 2 ausgehend
    [5, 7, 3, None, 5, 2],       # Kanten von 3 ausgehend
    [None, None, 12, 5, None, 5], # Kanten von 4 ausgehend
    [None, 4, None, 2, 5, None]     # Kanten von 5 ausgehend
]
graph = Graph(knoten, directed=False
for i in range(len(knoten)):
    for j in range(i+1,len(knoten)):
        if graph[i][j] is not None:
            g.add_edge(i,j,graph[i][j]))

Beispielimplementierung: Dijkstra

Zu guter letzt wird die Graphenklasse verwendet, um den wunderbaren Dijkstraalgorithmus zu implementieren.

import sys
def dijkstra_kuerzeste_distanz(g : Graph, start_node, goal_node):

    # Initialisierung : Kürzeste Distanz zu allen Knoten = unendlich
    kuerzeste_dist = [sys.maxsize for _ in range(g.nr_nodes)]
    kuerzeste_dist[start_node] = 0 # Ausser beim Startknoten

    # Alle Knoten sind unbetrachtet
    unbetrachtet = [i for i in range(g.nr_nodes)]

    while len(unbetrachtet) > 0:

        # Finde den nächsten zu betrachtenden Knoten
        # d.h. den, der am schnellste von start_node aus erreichbar ist
        naechster_kn = unbetrachtet[0]
        naechster_kn_idx = 0
        for i,knoten in enumerate(unbetrachtet):
            if kuerzeste_dist[knoten] < kuerzeste_dist[naechster_kn]:
                naechster_kn= knoten 
                naechster_kn_idx = i
        
        if naechster_kn == goal_node:
            # Keine Chance den kürzesten Pfad noch zu verbessern.
            # Wir sind fertig
            return kuerzeste_dist[naechster_kn]
        
        # Entferne den Knoten aus den unbetrachteten Knoten
        unbetrachtet.pop(naechster_knoten_idx)
        
        for verbl_kn in unbetrachtet:
            if not g.edge_exists(naechster_kn, verbl_kn):
                # Es gibt keine Kante zwischen den Knoten
                continue
            
            dist = kuerzeste_dist[naechster_kn] + g.get_weight(naechster_kn, verbl_kn)
            if dist < kuerzeste_dist[verbl_kn]:
                kuerzeste_dist[verbl_kn] = dist

Wollen wir die kürzeste Distanz zwischen Knoten 0 und 4 finden, gehen wir wie folgt vor:

# (für das o.g. Beispiel: 9)
print(dijkstra_kuerzest_distanz(g,0,4))